递归与分治

一、分治法

分治法思想

1. 将要解决的较大规模的问题不断地分割成更小规模的子问题，直到能够很容易地得到子问题的解。

2. 对小规模的问题进行求解

3. 将小问题的解合并为一个更大规模的问题的解，由子问题逐步求出原来问题的解。

4. 分治法是自顶向下的分解问题

• https://www.zhihu.com/question/27363814

分治法的使用条件

1. 原问题可分割成k个子问题，1<k<=n

2. 这些子问题都可解

3. 可利用这些子问题求出原问题的解

分治法的例子

棋盘覆盖问题：

• https://www.jianshu.com/p/97b09ef06735

归并排序：

 
#include <stdlib.h>
#include <stdio.h>
 
void Merge(int sourceArr[],int tempArr[], int startIndex, int midIndex, int endIndex)
{
    int i = startIndex, j=midIndex+1, k = startIndex;
    while(i!=midIndex+1 && j!=endIndex+1)
    {
        if(sourceArr[i] > sourceArr[j])
            tempArr[k++] = sourceArr[j++];
        else
            tempArr[k++] = sourceArr[i++];
    }
    while(i != midIndex+1)
        tempArr[k++] = sourceArr[i++];
    while(j != endIndex+1)
        tempArr[k++] = sourceArr[j++];
    for(i=startIndex; i<=endIndex; i++)
        sourceArr[i] = tempArr[i];
}
 
//内部使用递归
void MergeSort(int sourceArr[], int tempArr[], int startIndex, int endIndex)
{
    int midIndex;
    if(startIndex >= endIndex)   return;    // 解决一个元素的问题
    midIndex = (startIndex + endIndex) / 2;     //中间点作为分割点
    MergeSort(sourceArr, tempArr, startIndex, midIndex);    // 分治解决问题1
    MergeSort(sourceArr, tempArr, midIndex+1, endIndex);    // 分治解决问题2
    Merge(sourceArr, tempArr, startIndex, midIndex, endIndex);    //合并a[left:mid], a[mid+1, right]
}
 
int main(int argc, char * argv[])
{
    int a[8] = {50, 10, 20, 30, 70, 40, 80, 60};
    int i, b[8];
    MergeSort(a, b, 0, 7);
    for(i=0; i<8; i++)
        printf("%d ", a[i]);
    printf("\n");
    return 0;
}

二、递归

递归算法的定义

1. 直接或间接地调用自身的算法称为递归算法

2. 用函数自身给出定义的函数称为递归函数

3. 使用被定义对象的自身来为其下定义称为递归定义

4. 边界条件和递归方法是递归函数的二要素

递归举例

Fibonacci数列（斐波那契数）：

//第n个Fibonacci数可递归地计算如下：

int fibonacci(int n)
   {
       if (n <= 1) return 1;
       return fibonacci(n-1)+fibonacci(n-2);
   }

Ackerman（阿克曼函数）：

• Ackerman函数是一个双递归函数，当一个函数以及它的一个变量是由函数自身定义时，称为双递归函数。

int ackerman(int n,int m){
	int F;
	if(n==1 && m==0)
		F = 2;
	else if(n==0 && m>=0)
		F = 1;
	else if(n>=2 && m==0)
		F = n+2;
	else
		F = ackerman(ackerman(n-1,m),m-1);
	return F;
}

全排列：

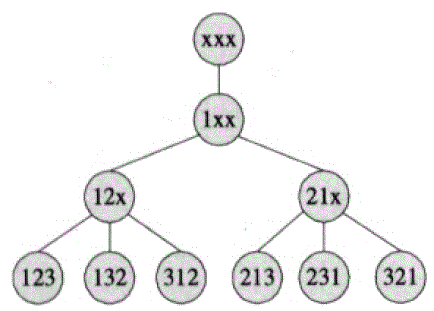
void perm(int m) {
	if(m==0){
		for(int i=0;i<arr.length;i++){
			System.out.print(arr[i]+" ");
		}
		System.out.println();
		return;
	}
	else{
		for(int i=0;i<arr.length;i++){
			if(arr[i]==0){
				arr[i] = m;
				perm(m-1);
				arr[i] = 0;
			}
		}
	}
}

整数划分

找到正整数n的划分个数 将最大加数不大于m的划分个数记作q(n,m)

• https://www.cnblogs.com/hoodlum1980/archive/2008/10/11/1308493.html

/**
例如正整数6有如下11种不同的划分：
    6；
    5+1；
    4+2，4+1+1；
    3+3，3+2+1，3+1+1+1；
    2+2+2，2+2+1+1，2+1+1+1+1；
    1+1+1+1+1+1。
**/

unsigned long  GetPartitionCount(int n, int max)
{
    if (n == 1 || max == 1)
        return 1;
    else if (n < max)
        return GetPartitionCount(n, n);
    else if (n == max)
        return 1 + GetPartitionCount(n, max-1);
    else
        return GetPartitionCount(n,max-1) + GetPartitionCount(n-max, max);
}

Hanoi塔问题

设A,B,C是3个塔座 开始时，在塔座A上有一叠共n个圆盘，这些圆盘自下而上，由大到小地叠在一起 各圆盘从小到大编号为1,2,…,n 现要求将塔座A上的这一叠圆盘移到塔座B上，并仍按同样顺序叠置

规则1：每次只能移动1个圆盘 规则2：任何时刻都不允许将较大的圆盘压在较小的圆盘之上 规则3：在满足移动规则1和2的前提下，可将圆盘移至A,B,C中任一塔座上

void hanoi(int n, int a, int b, int c) {
   if (n > 0) {
	  hanoi(n-1, a, c, b);
	  move(a,b);
	  hanoi(n-1, c, b, a);
   }
}