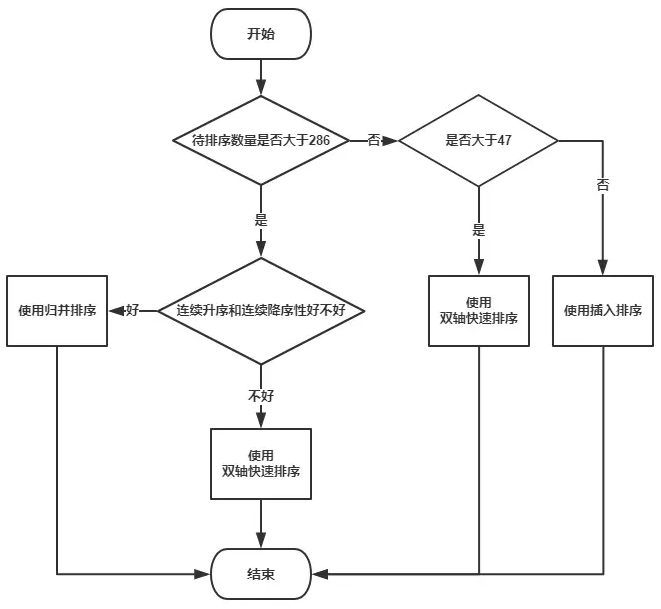
排序算法
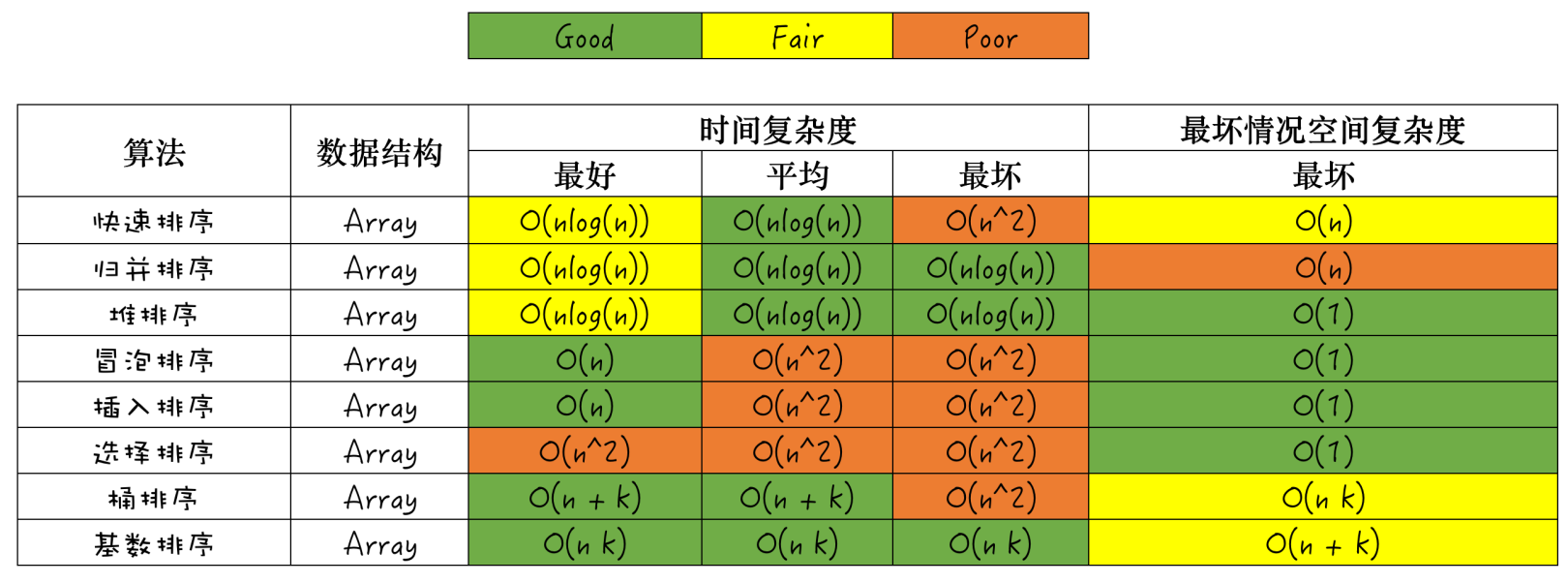
- 数据结构可视化:https://www.cs.usfca.edu/~galles/visualization/Algorithms.html
- *八大排序:https://juejin.cn/post/6844903687932887053#heading-7
- *leetcode排序解析:https://leetcode.cn/problems/sort-an-array/solution/fu-xi-ji-chu-pai-xu-suan-fa-java-by-liweiwei1419/
JDK算法
冒泡排序
算法效率
- 稳定算法
| 平均时间复杂度 | 最好情况 | 最坏情况 | 空间复杂度 |
|---|---|---|---|
| O(n2) | O(n) | O(n2) | O(1) |
快排(重点)
基本思想
- https://juejin.cn/post/6844903640340267022
- 优化思路:https://juejin.cn/post/6844903576037244935
快速排序(Quicksort)是对冒泡排序的一种改进,借用了分治的思想,基本思路是:
- 每次选择一个数,将所有小于该数的元素放到该数的前面,大于的放到其后面。(每次都确定一个元素的位置)
- 递归实现
JDK的Arrays.sort采用了双轴快速排序
快排的实现方式:
- 基本快排
- 双指针快排
- 三指针快排
基本快排和双指针快排的区别:[2, 1, 3, 1, 3, 1],对于普通快排,需要swap三次,对于双指针快排,需要swap一次
代码实现
只记住第一种和第二种写法就行,不要记零的写法,所以整个过程中涉及到的对象间的调整都是swap,记住!
- 写法零:填坑法(双指针)
public static void sort(int arr[], int low, int high) {
if (arr == null || arr.length <= 0) {
return;
}
if (low >= high) {
return;
}
int left = low;
int right = high;
int temp = arr[left]; //挖坑1:保存基准的值
while (left < right) {
while (left < right && arr[right] >= temp) {
right--;
}
arr[left] = arr[right]; //坑2:从后向前找到比基准小的元素,插入到基准位置坑1中
while (left < right && arr[left] <= temp) {
left ++;
}
arr[right] = arr[left]; //坑3:从前往后找到比基准大的元素,放到刚才挖的坑2中
}
arr[left] = temp; //基准值填补到坑3中,准备分治递归快排
sort(arr, low, left-1);
sort(arr, left + 1, high);
}
- 写法一:基本快速排序
- partition方法:找到基准下标,该基准左边都是小于基准的值,右边都是大于基准的值
public int[] sortArray(int[] nums) {
quickSort(nums, 0, nums.length - 1);
return nums;
}
private void quickSort(int[] nums, int left, int right){
if(left >= right){
return;
}
int pIndex = partition(nums, left, right);
quickSort(nums, left, pIndex - 1);
quickSort(nums, pIndex + 1, right);
}
private int partition(int[] nums, int left, int right){
int pivot = nums[left];
int lt = left;
for(int i = left + 1;i <= right;i ++){
if(nums[i] <= pivot){
lt ++;
swap(nums, i, lt);
}
}
swap(nums, lt, left);
return lt;
}
private void swap(int[] nums, int left, int right){
int tmp = nums[left];
nums[left] = nums[right];
nums[right] = tmp;
}
- 写法二:双指针(指针对撞)快速排序
public int[] sortArray(int[] nums) {
quickSort(nums, 0, nums.length - 1);
return nums;
}
private void quickSort(int[] nums, int left, int right){
if(left >= right){
return;
}
int pIndex = partition(nums, left, right);
quickSort(nums, left, pIndex - 1);
quickSort(nums, pIndex + 1, right);
}
private int partition(int[] nums, int left, int right){
int pivot = nums[left];
// lt从left开始,lt在开始移动后代表第一个从左往右 > povit的元素,没有移动时停留在 <= pivot的元素上(swap需要),如果从left + 1开始,没有 <= pivot的数时会被强制swap,导致出错
int lt = left;
// gt移动后表示第一个 < povit的元素,不care不移动时候的指向元素
int gt = right;
while(lt < gt){
// lt从left开始,得先遍历gt的,这样即使遇到1,2,3,4这种已经有序的,也可以保证lt没有移动,因为如果是lt先遍历,无论如何都会往下走一位,这样left和lt会被强制替换导致出问题
while(lt < gt && nums[gt] >= pivot){
gt --;
}
while(lt < gt && nums[lt] <= pivot){
lt ++;
}
swap(nums, lt, gt);
}
swap(nums, left, lt);
return lt;
}
private void swap(int[] nums, int left, int right){
int tmp = nums[left];
nums[left] = nums[right];
nums[right] = tmp;
}
算法效率
-
不稳定
-
最坏情况:数组有序(正序或倒序),这样每次partition后都分为一个为空、一个为(n-1)个数的数组,最终O(n^2)
-
最好情况:每次都能平均分割,O(nlogn)
-
平均情况:O(n*logn)
-
空间复杂度:主要由递归而产生的对栈空间的影响
- 最好:O(logn):pivot为中间值,树平衡
- 最坏:O(n):数组基本有序,取第一个数作为pivot会导致生成树不平衡,数高度=数组长度
- 平均:O(logn)
| 平均时间复杂度 | 最好情况 | 最坏情况 | 空间复杂度 |
|---|---|---|---|
| O(nlogn) | O(nlogn) | O(n2) | O(logn) |
插入排序
算法思路
算法实现
if (a == null || a.length == 0) {
return;
}
for (int i = 1; i < a.length; i++) {
int j = i - 1;
int temp = a[i]; // 先取出待插入数据保存,因为向后移位过程中会把覆盖掉待插入数
while (j >= 0 && a[j] > temp) { // 如果待是比待插入数据大,就后移
a[j+1] = a[j];
j--;
}
a[j+1] = temp; // 找到比待插入数据小的位置,将待插入数据插入
}
算法效率
- 稳定
| 平均时间复杂度 | 最好情况 | 最坏情况 | 空间复杂度 |
|---|---|---|---|
| O(n2) | O(n) | O(n2) | O(1) |
希尔排序
算法效率
- 不稳定
选择排序
算法思路
每次选择最小的数的下标,并将其取出排序
算法实现
public int[] sortArray(int[] nums) {
for(int i = 0;i < nums.length;i ++){
int min = i;
for(int j = i + 1;j < nums.length;j ++){
if(nums[min] > nums[j]){
min = j;
}
}
swap(nums, min, i);
}
return nums;
}
private void swap(int[] nums, int left ,int right){
int tmp = nums[left];
nums[left] = nums[right];
nums[right] = tmp;
}
算法效率
- 不稳定(涉及到swap,例如{5,5,2})
| 平均时间复杂度 | 最好情况 | 最坏情况 | 空间复杂度 |
|---|---|---|---|
| O(n2) | O(n2) | O(n2) | O(1) |
归并排序(重点)
代码实现
public int[] sortArray(int[] nums) {
if(nums.length <= 1){
return nums;
}
int num = nums.length / 2;
int[] left = Arrays.copyOfRange(nums, 0, num);
int[] right = Arrays.copyOfRange(nums, num, nums.length);
return merge(sortArray(left), sortArray(right));
}
private int[] merge(int[] left, int[] right){
int len1 = left.length;
int len2 = right.length;
int i = 0, j = 0, k = 0;
int[] res = new int[len1 + len2];
while(i < len1 && j < len2){
if(left[i] < right[j]){
res[k++] = left[i++];
}else {
res[k++] = right[j++];
}
}
while(i < len1){
res[k++] = left[i++];
}
while(j < len2){
res[k++] = right[j++];
}
return res;
}
算法效率
- 稳定
| 平均时间复杂度 | 最好情况 | 最坏情况 | 空间复杂度 |
|---|---|---|---|
| O(nlogn) | O(nlogn) | O(nlogn) | O(n) |
基数排序
算法思路
如下图所示,依次对从高位到低位上的元素进行排序(桶思想)。
适用场景:
- 数据范围较小,建议在小于1000
- 每个数值都要大于等于0
基数排序 vs 计数排序 vs 桶排序
这三种排序算法都利用了桶的概念,但对桶的使用方法上有明显差异:
- 基数排序:根据键值的每位数字来分配桶
- 计数排序:每个桶只存储单一键值
- 桶排序:每个桶存储一定范围的数值
算法效率
- 稳定
| 平均时间复杂度 | 最好情况 | 最坏情况 | 空间复杂度 |
|---|---|---|---|
| O(d*(n+r)) | O(d*(n+r)) | O(d*(n+r)) | O(n+r) |
堆排序(重点)
- 堆排序动画:https://www.bilibili.com/video/BV1B64y1975b?vd_source=db044ebd2a1b441023aaee25eb452c6c
基本思想
- 将待排序序列构造成一个大顶堆,此时,整个序列的最大值就是堆顶的根节点。
- 将堆顶节点与最后一个节点进行swap,并剔除出堆
- 调整替换后的堆,让堆顶重回最大元素
代码实现
public int[] sortArray(int[] nums) {
int len = nums.length;
// 构建大根堆,从最后一个非叶子结点开始
for(int i = (len - 1) / 2;i >= 0;i --){
adjustHeap(nums, i, len - 1);
}
// 替换根顶和末尾的元素,并重新调整,大根堆保证每个节点都大于其左右节点(即子树的根节点是最大的值)
for(int i = len - 1;i >= 0;i --){
swap(nums, i, 0);
adjustHeap(nums,0, i - 1);
}
return nums;
}
public void adjustHeap(int[] nums, int k,int end){
// 左叶子结点
while(2 * k + 1 <= end){
int j = 2 * k + 1;
if(j + 1 <= end && nums[j + 1] > nums[j]){
j ++;
}
if(nums[j] > nums[k]){
swap(nums, j, k);
// 该子树被调整了,需要重新构建
k = j;
}else {
// 已经为最大值
break;
}
}
}
private void swap(int[] nums, int left, int right){
int tmp = nums[left];
nums[left] = nums[right];
nums[right] = tmp;
}
算法效率
- 不稳定
| 平均时间复杂度 | 最好情况 | 最坏情况 | 空间复杂度 |
|---|---|---|---|
| O(nlogn) | O(nlogn) | O(nlogn) | O(1) |